How To Take Out Negative Exponents
When n is a positive integer exponentiation corresponds to repeated multiplication of the base. If the exponent is an odd positive integer the result will again have the same magnitude but.

Exponents Are Used To Represent The Repeated Multiplication Of A Number By Itself Some Rules Of Exponents Are G Exponents Negative Numbers Rules Quotient Rule
I took a practice Accuplacer test and realized that I did not remember hardly any of my high school math so I took the Accuplacer College Level Math prep course.

How to take out negative exponents. If the exponent is an even positive integer the values will be equal regardless of a positive or negative base. We will close out this section with a more general version of the first property of radicals. Lets start with simple example.
Lets take a look. In fact this is a neat part of any exponential graph. A positive exponent tells us how many times to multiply a base number and a negative exponent tells us how many times to divide a base number.
So if they give you say x 36 then x had better not be negative because x 3 would still be negative and you would be trying to take the sixth root of a negative number. That is b n is the product of multiplying n bases. If they give you x 46 then a negative x becomes positive because of the fourth power and is then sixth-rooted so it becomes x 23 by reducing the fractional power.
8 2 8 8 64. The sentence means 1 second ago we were at half our current amount 121. I placed past College Algebra.
In 8 2 the 2 says to use 8 twice in a multiplication so 8 2 8 8 64. I have been out of high school for 30 years and am going to take a few college courses. If going forward grows by a scaling factor going backwards should shrink by it.
Following the instructions in the table lets create the formulas we need to use exponents. A logarithm is the opposite of a powerIn other words if we take a logarithm of a number we undo an exponentiation. First let us look at whole number exponents.
Exponents with negative bases raised to positive integers are equal to their positive counterparts in magnitude but vary based on sign. Recall that negative exponents indicates that we need to move the base to the other side of the fraction line. A negative exponent tells you to divide the number 1 by the base number.
Exponents are used when a number is multiplied by itself. This is explained in the Solving Basic Exponents method below. Using negative power values results in fractions and when these fractions have exponents applied to them we get Decay.
X to the 8th power is the answer which is c. Exponents are also called Powers or Indices. Going out to positive infinity these will all be zero in the limit and so will no longer cause problems.
Learn how to rewrite expressions with negative exponents as fractions with positive exponents. Notice that in doing this factoring all the remaining exponentials now have negative exponents and we know that for this limit ie. Negative seconds means going back in time.
The exponent is usually shown as a superscript to the right of the base. For 3 squared we input 3 2 which gives us 9. Subtracting a negative you change the sign.
On the other hand if they give you something. An easy way to remember this is that a negative is the opposite of a positive and division is the opposite of multiplication. For example 4 13 is the 3rd root cube root of 4.
A fractional exponentspecifically an exponent of the form 1nmeans to take the nth root instead of multiplying or dividing. In a Decay process the amount involved drops off fairly quickly at the start but then the drop off becomes slower and slower. To begin we must understand how to read and write a number in scientific notation.
The 1 s in the simplifications above are for claritys sake in case its been a while since you last worked with negative powers. A little later well look at negative exponents in the bottom of a fraction. So it is 5 -3.
Also called Radicals or Rational Exponents Whole Number Exponents. 8 2 could be called 8 to the power 2 or 8 to the second power or simply 8 squared. Now were on a roll what does a negative exponent mean.
Lets see if we can apply what we know about negative number what we know about negative numbers and we know about exponents to apply exponents to negative numbers so lets first think about lets just must say we have negative three lets first think about what it means to raise it to the first power well that literally means just taking a negative three just taking a negative three and there. Instead of writing out 4 4 4 4 4 however you can simply write out 45. Exponents make it easier to write.
2 when u have exponents that are divided you need to subtract those exponents. Like previous examples we have a simple worksheet that highlights several cell references. We can rewrite negative exponents like xⁿ as 1 xⁿ.
The first formula doesnt use any cell references. We can now take the limit of the two factors. The exponent of a number says how many times to use the number in a multiplication.
The exponent of a number says how many times to use the number in a multiplication. Exponentiation is a mathematical operation written as b n involving two numbers the base b and the exponent or power n and pronounced as b raised to the power of n. Recall that when we first wrote down the properties of radicals we required that a be a positive number.
Lets take a look at an example. Scientific Notation is a way for us to write and use very large or very small numbers easily. In fact youll quickly see that working in Scientific Notation enables us to work effectively all while avoiding careless mistakes with decimals.
However if you are on a track that will take you into a Calculus class you will find that rationalizing is useful on occasion at that level. Change the -3 sign into positive and the problem then becomes 5 3 which is 8. For example 2⁴ 1 2⁴ 116.

Rules For Exponents An Explanation For How Negative Exponents Work Math Exponentrules Negative Exponents High School Math Exponents
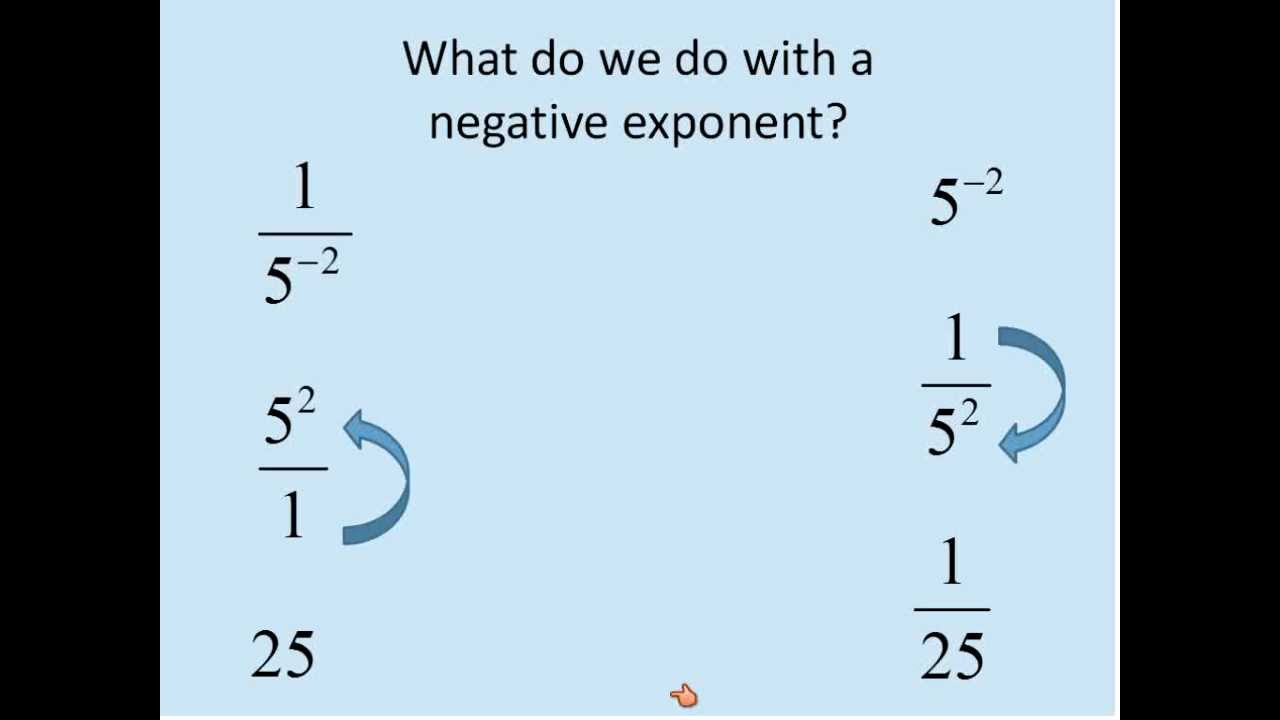
Youtube Negative Exponents Exponents Math

Circuit Training Negative Exponents In 2021 Negative Exponents Exponents Algebraic Expressions

Integer Exponent Rules Poster Exponent Rules Teaching Algebra Math Charts

How To Do Negative Exponents 25 Amazing Examples Negative Exponents Exponents Math Methods

Zero And Negative Exponents Negative Exponents Exponents Zero Exponents

Exponent Rules Worksheet Exponent Rules Exponent Worksheets Negative Exponents

Pin By Gecsa Fg On Year 9 Mathematics Negative Exponents Mathematics Exponents

Zero And Negative Exponents Zero Exponents Negative Exponents Simplifying Expressions With Exponents

Negative Exponents And Zero Exponents Exponent Worksheets Negative Exponents Exponents Math

Pin On Pre Calculus Lesson Ideas

Negative Exponents Journal Entry School Algebra High School Math Teaching Exponents

Algebra Simplifying Complex Fractions Algebra Fractions Negative Exponents





